This post is part of my Game Physics Series.
As mentioned earlier, all collision detection algorithms are essentially determining if the CSO of two shapes contains the origin. The collision detection I am going to introduce to you here, the Gilbert-Johnson-Keerthi (GJK) algorithm, is no different.
GJK is one of the most popular collision detection algorithms, because it is very efficient and intuitive (once you get it, of course). It basically attempts to find a subset, or a “simplex” to be precise, of the CSO that contains the origin. A simplex in n-dimension, by definition, is a minimal geometry in n-dimension that can be tightly tiled to fill up the space; for instance, a triangle is a 2D simplex, and tetrahedron is a 3D simplex. Inside the CSO of two colliding shapes, we can find a point (0D simplex), a line (1D simplex), a triangle (2D simplex), or a tetrahedron (3D simplex) that contains the origin.
Here’s GJK in its entirety:
- Initialze simplex to empty set (-1D simplex, technically).
- Use an initial direction to find a support point of the CSO.
- Add that support point to simplex (now the simplex has a single vertex).
- Find the closest point in the simplex to the origin.
- If the closest point is the origin, then the CSO contains the origin and the two objects are colliding. End GJK.
- Otherwise, reduce the simplex to the lowest dimension possible that still contains the closest point by discarding vertices.
- Use the direction from the closest point to the origin to find a new support point.
- If the new support point is not further along the search direction than the closest point, the two objects are not colliding. End GJK.
- Add support point to simplex as a new vertex. Go to 4.
Visual Example in 2D
A picture is worth a thousand words. Let’s look at what is going on visually in 2D (the highest-dimension simplex we will get here would be a triangle).
Suppose we have a CSO that is shaped like an ellipse. The cross indicates the origin. The arrow is the initial direction we pick to find the first support point (the black dot).

The simplex now only contains one vertex, so the vertex is the closest point to the origin. The next search direction is from the vertex to the origin. A new support point is found and added to the simplex as a new vertex. The simplex is now a line segment.
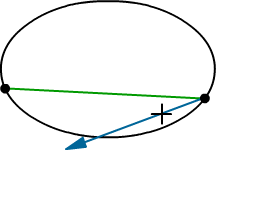
The origin is not on the line segment, so we continue the algorithm. The search direction points from the closest point on the line segment to the origin towards the origin. The direction is basically the line normal. A third support point is found and added to the simplex. Now the simplex is a triangle.
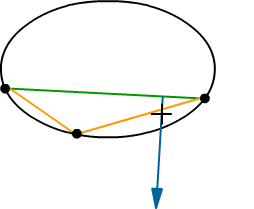
The triangle does not contain the origin. And the closest point to the origin in the triangle lies on the bottom right side. Thus, the top left vertex of the simplex is discarded. The simplex is now a line segment again. The direction from the closest point to the origin on the line towards the origin is used to find a new support point.
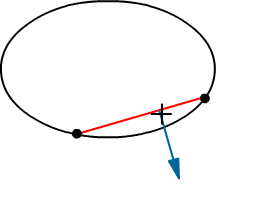
With the new support point added to the simplex, the simplex is now a triangle again.
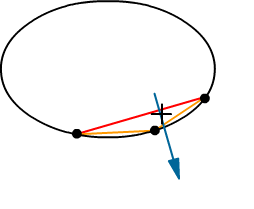
This time, the simplex contains the origin, so we end the GJK algorithm and conclude that the CSO contains the origin.

If during any iteration we find that the new support point is not further along the search direction than the existing simplex vertices, then the origin must be outside the CSO, and we can terminate GJK.
For GJK in 3D, not only can the simplex reduction phase end up with a point or a line segment, it can also end up with a triangle due to the one extra dimension compared to 2D.
End of GJK
GJK only tells us whether two shapes collide (it essentially returns true or false). The next step is to generate contact information required during the resolution phase in the physics engine.
Recall that the support function result of a CSO is a combination of the results of support functions of two individual shapes. In order to properly generate the required contact information, we will need to keep track of both the individual results and the combined result.
Basically, when we store this:
![]()
We also want to store these:
![]()
![]()
I will elaborate on this matter when I talk about the Expanding Polytope Algorithm (EPA).
Extra
In light of a recent discussion on Reddit, I’d like to also point out another benefit of keeping track of individual support function results of each shape. Even if the two shapes don’t collide, we can further use this information to find out the closest distance and closest points between the shapes.
We start with the final simplex we end up with after deciding that the two shapes are not colliding. Find the primitive in the simplex that contains the closest point to the origin, which could be a vertex, edge, or triangle. The distance between the closest point to the origin and the origin itself is the closest distance between the two shapes.
Next, we can compute the closest points between the two shapes using the primitive:
- If the primitive is a vertex, then it is a support function result in the CSO, and the individual corresponding support function results from each shape are the closest points between the shapes.
- If the primitive is an edge, then it is formed by two vertices, so the closest point to the origin is a linear interpolation between the two vertices, which are in turn support function results in the CSO. Compute the linear interpolation coefficient. For each shape, get the two corresponding vertices used to form the two vertices of the primitive, and apply the same linear interpolation using the previously calculated coefficient. This gives you the closest point in each shape to the other shape.
- If the primitive is a triangle, then it is formed by three vertices, so the closest point to the origin is a linear combination among the three vertices, which are in turn support function results in the CSO. Compute the linear combination coefficients (barycentric coordinate). For each shape, get the three corresponding vertices used to form the three vertices of the primitive, and apply the same linear combination using the previously calculated coefficients. This gives you the closest point in each shape to the other shape.


Hi Allen, I’ve ran into a weird edge case at the start of the algorithm when the simplex contains two points (let’s call them v0 and v1).
I calculate the next search direction by finding a vector normal to this line segment in the direction of the origin thusly:
search_dir = (v1-v0) x (-v0) x (v1-v0)
(cross products are evaluated left to right)
However, if the origin lies on the line segment v1-v0 then this returns a zero vector as the new search direction. This is happening with two unit cubes at positions (0,0,0) and (0.9,0,0). What should I do in this case to calculate a correct search direction? Thanks.
In this degenerate case, I believe any direction normal to the line segment will do the trick.
I am trying to find the minimum distance between two boxes in 3D using GJK distance algo. I would like to find the point (on the closest face of Minkowski Sum) closest to origin. I have GJK up and running and I get a final triangle-simplex on the closest face of minkowski sum. I then want to find the closest point on this face to origin (using point-plane distance check). The problem is that the point found might not be inside the face. It will for sure be on the plane, but could be outside the face. So I will need a check whether the point found is inside or outside the face. This should be easy to figure out if I only knew the fourth (4) minkowski sum point on this face. (I can get a triangle on closest face from GJK). Since I am dealing with OBBs (find minimum distance between 2 OBBs in 3D) my minkowski sum shape will also be an OBB. So how can I find this last point for the current closest face? I get a triangle from GJK (3 points in minkowski sum) but I actually need all 4 points in order to know if the closest point found is actually inside the rectagle based face. I hope you understand my question and could give some help. Thanks!
If the projection of origin onto the plane containing the triangle (2D simplex) is outside the triangle, the closest point on the triangle to the origin should be on one of the triangle’s edges or vertices. Then you can obtain the fourth point to form a tetrahedron (3D simplex) by evaluating the support function with the support vector being the vector pointing from the closest point on the triangle to the origin. I don’t see why you would handle this differently if you know beforehand that both your shapes are OBBs. I hope this answers your question.
P.S. If the 2 OBBs are not aligned, their Minkowski sum will not be an OBB.