Game Math: Quaternion Basics

Posted on April 9, 2014 by Allen Chou

This post is part of my Game Math Series.

A quaternion is a very useful mathematical object devised by Sir William Rowan Hamilton as an extension to complex numbers. It is often used to compactly represent 3D orientations with just four floating-point numbers, as opposed to using a 3-by-3 matrix that contains nine floating-point numbers, and it has other nice properties that I will talk about later.

As its name suggests, a quaternion is composed of four components, one in the real part, and the other three in the imaginary part. A quaternion is usually denoted as:

    \[ q = w + xi + yj + zk, \]

where w is the real part, (i, j, k) denotes the three imaginary axes, and (x, y, z) denotes the three imaginary components.

For brevity, I will use the notation below to represent a quaternion:

    \[ q = [w, \overrightarrow{v}], where \overrightarrow{v} = (x, y, z). \]

The Fundamental Formula for Quaternions

Below is the fundamental formula that governs the arithmetics of quaternions:

    \[ i^2 = j^2 = k^2 = ijk = -1 \]

With this formula, we can derive the following identities:

    \begin{flalign*} ij &= k \\ jk &= i \\ ki &= j \\ ji &= -k \\ kj &= -i \\ ik &= -j \\ \end{flalign*}


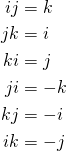
Thus, if we expand the product of two quaternions, we will arrive at the quaternion multiplication formula:

    \begin{flalign*} q_1 q_2 &= (w_1 + x_1 i + y_1 j + z_1 k) (w_2 + x_2 i + y_2 j + z_2 k) \\ &= [w_1, \overrightarrow{v_1}] [w_2, \overrightarrow{v_2}] \\ &= [(w_1 w_2 - \overrightarrow{v_1} \cdot \overrightarrow{v_2}), (w_1 \overrightarrow{v_2} + w_2 \overrightarrow{v_1} + \overrightarrow{v_1} \times \overrightarrow{v2})] \\ \end{flalign*}

Note that quaternion multiplication is associative:

    \[ q_1 q_2 q_3 = (q_1 q_2) q_3 = q_1 (q_2 q_3) \]

but generally not commutative:

    \[ q_1 q_2 \neq q_2 q_1 \]

Adding and subtracting two quaternions are just like adding and subtracting two 4D vectors:

    \[ q_1 \pm q_2 = [w_1 \pm w_2, \overrightarrow{v_1} \pm \overrightarrow{v_2}] \]

Multiplying a quaternion by a scalar is as simple as multiplying individual component by the scalar:

    \[ c q = [ c w, c \overrightarrow{v}] \]

The dot product of two quaternions is the sum of products of corresponding components:

    \[ q_1 \cdot q_2 = w_1 w_2 + x_1 x_2 + y_1 y_2 + z_1 z_2 \]

Unit Quaternions

The magnitude of a quaternion is calculated as follows:

    \[ || w, \overrightarrow{v} || = \sqrt{w^2 + x^2 + y^2 + z^2} \]

A unit quaternion has a magnitude of one. The product of two unit quaternions is also a unit quaternion. To normalize a quaternion means dividing each quaternion component by the quaternion’s magnitude.

For convenience, game developers usually just work with unit quaternions. After many multiplications, a quaternion can become non-normalized, so we sometimes need to re-normalize a quaternion to make sure it stays normalized. The approximation technique described in this post can be used to re-normalize an almost-normalized quaternion without using the square root function and floating-point division.

Quaternion Inverses

For a quaternion q, its multiplicative inverse (or inverse for short) is denoted q^{-1} and satisfies the property below:

    \[ q q^{-1} = q^{-1} q = 1 \]

If the quaternion q = [w, \overrightarrow{v}] is a unit quaternion, then its inverse is just its conjugate:

    \[ q^{-1} = \overline{q} = [w, -\overrightarrow{v}] \]

Just like that, as easy as negating the imaginary part. This is one of the many reasons why game developers prefer working with unit quaternions. Otherwise, the inversion process would involve a floating-point division by the magnitude of the quaternion.

Also, the inverse of a quaternion product of two quaternions would be equal the individual quaternion inverses multiplied in reverse order:

    \[ (q_1 q_2)^{-1} = q_2^{-1} q_1^{-1} \]

Proof:

    \begin{flalign*} (q_1 q_2)^{-1} (q_1 q_2) &= q_2^{-1} q_1^{-1} q_1 q_2 \\ &= q_2^{-1} (q_1^{-1} q_1) q_2 \\ &= q_2^{-1} q_2 = 1 \end{flalign*}

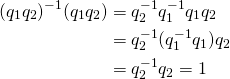
3D Orientations

Every orientation in 3D can be represented using the axis-angle representation, and there is a mapping between an axis-angle pair and a unit quaternion.

For an orientation represented by an axis \overrightarrow{n} and an angle \theta, the corresponding unit quaternion is:

    \[ q = [cos\frac{\theta}{2}, \overrightarrow{n} sin\frac{\theta}{2}] \]

When we have a 3D vector \overrightarrow{r} and would like to rotate it by the orientation represented by a quaternion q, we simply have to perform two quaternion multiplications:

    \[ [0, \overrightarrow{r}'] = q [0, \overrightarrow{r}] q^{-1}, \]

where \overrightarrow{r}' is the rotated vector.

Rotation Concatenation

Concatenation of two rotations represented by two quaternions, q_1 and q_2 (in this order), is as simple as multiplying them in the reverse order of concatenation: q_2 q_1.

So the formula below:

    \[ [0, \overrightarrow{r}''] = (q_2 q_1) [0, \overrightarrow{r}] (q_2 q_1)^{-1} \]

would give the resulting vector \overrightarrow{r}'' as the vector \overrightarrow{r} rotated first by q_1 and then q_2, which can be seen in the more detailed computation steps:

    \begin{flalign*} [0, \overrightarrow{r}''] &= (q_2 q_1) [0, \overrightarrow{r}] (q_2 q_1)^{-1} \\ &= q_2 q_1 [0, \overrightarrow{r}] q_1^{-1} q_2^{-1} \\ &= q_2 (q_1 [0, \overrightarrow{r}] q_1^{-1}) q_2^{-1} \\ &= q_2 [0, \overrightarrow{r}'] q_2^{-1} \end{flalign*}

where \overrightarrow{r}' is the intermediate vector of \overrightarrow{r} rotated by q_1.

Slerp

Slerp (spherical linear interpolation) is a very important quaternion operation. It allows you to interpolate between two orientations along the “shortest path” if the two quaternions used are of the same magnitude (another good reason to work with only unit quaternions). This is a non-trivial task if you represent 3D orientations using rotation matrices or Euler angles. Below is the formula for slerping from a quaternion q_1 to another quaternion q_2 using an interpolation parameter t:

    \[ Slerp(q_1, q_2, t) = \frac{sin((1 - t)\Omega)}{sin\Omega}q_1 + \frac{sin(t\Omega)}{sin\Omega}q_2, \, 0 \le t \le 1, \]

where \Omega is the “angle” between the two unit quaternions:

    \[ \Omega = cos^{-1}(q_1 \cdot q_2) \]

One nice thing about slerp is the linearity of interpolation with respect to the parameter t. If t = 0.5, then the slerp result is a quaternion that represents an orientation exactly 50% between the two quaternions. If t varies at a constant rate, then the orientation represented by the slerp result also varies at a constant angular velocity.

There is one caveat, though. Exactly two quaternions can map to the same orientation, namely q = [w, \overrightarrow{v}] and -q = [-w, -\overrightarrow{v}]. It makes sense if you think about it: rotating around an axis by an angle gives the same result as rotating around the opposite axis by the reverse angle. When performing slerp, we need to make sure the quaternion we are interpolating towards is the “closer” one of the two opposite twins. This check is pretty easy and so is the fix. If the dot product of the two quaternions we are interpolating between is negative, that means we need to use the opposite twin of the target quaternion instead, i.e. replace q_2 with -q_2 if q_1 \cdot q_2 < 0.

End of Quaternion Basics

That’s it. I have covered the basic operations for quaternions, how to represent a 3D orientation using a quaternion, how to rotate a point using quaternions, and a nice tool called “slerp” to interpolate between two 3D orientations along the “shortest path”.

About Allen Chou

Physics / Graphics / Procedural Animation / Visuals
This entry was posted in Gamedev, Math. Bookmark the permalink.

1 Response to Game Math: Quaternion Basics

  1. katopz (@katopz) says:
    April 21, 2014 at 03:30

    Nice blog as always, I feeling lost at quaternion multiplication formula dot and cross product, my math completely rusted. 🙂

    Reply

Leave a Reply

This site uses Akismet to reduce spam. Learn how your comment data is processed.