Ming-Lun "Allen" Chou | 周明倫

This post is part of my Game Physics Series.

Dynamic AABB tree is a type of broadphase that is borderless, meaning that it does not impose a strict border limit as some other broadphases do, such as explicit grid and implicit grid.

It is very efficient in all aspects in terms of game physics, including ray casting, point picking, region query, and, most importantly, generating a list of collider pairs that are potentially colliding (which is the main purpose of having a broadphase).

In this post, I will explain how a dynamic AABB tree works and show you a sample implementation.

The Structure

First, let’s look at the basic concept of a dynamic AABB tree. From its name, you can already guess that it has something to to with storing AABB-related information in a tree structure, and it is dynamic at run time.

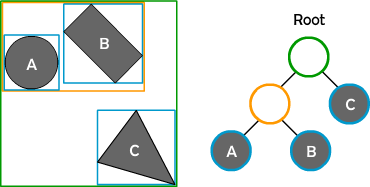
Each collider has its own AABB, and they are stored inside a binary tree as leaf nodes. Each internal node, a.k.a. branch node, holds its own AABB data that represents the union of the AABB of both of its children.

Visual aids are always better than plain text. The picture below shows a spatial configurations of several colliders and a visual representation of a possible corresponding tree structure.

Continue reading →

This post is part of my Game Physics Series.

Besides using slops, “warm starting” is also a very common technique used to make physics engines more stable. Warm starting works particularly well when your game has high “frame coherence”, which is usually the case.

Frame Coherence

Frame coherence is a measurement of how much your game scene changes across time steps. If the position and velocity of rigid bodies do not change a lot between two time steps, then these two frames have high frame coherence.

Having a high frame coherence has many implications, one of the most important ones is that the resolution result of the current time step will be very close to the result from the previous time step. So, if we cache the resulting impulses applied to each rigid body in the previous time step, we can apply the same impulses at the beginning of the resolution phase of the current time step before the real resolution logic takes place. This would make the entire physics system converge to a global solution faster. For instance, stacked boxes would settle faster with warm starting. Note that we only apply warm starting to contacts that last more than one time step. No warm starting is applied to a contact within the time step of the contact’s creation.

From my post about contact constraints, you already see that we have the information of total Lagrange Multiplier stored per contact. This information acts as our “cache” and is carried across time steps.

Continue reading →

This post is part of my Game Physics Series.

I previously hinted that there will be stability issues as I covered collision resolution. It is because the logic for collision resolution presented earlier is sort of “naive” in a sense that it tries to perfectly resolve all “conflicts”. Nothing is perfect. If you try to perfectly simulate a stack of boxes, you get jitters. This is when the concept of “slop” is introduced, where we become more forgiving to errors and give everything a little bit of leeway.

Penetration Slop

As mentioned in the previous post, Baumgarte Stabilization is a technique for correcting positional errors by applying just enough impulse to push penetrating colliders apart. Without slop, if two colliders are just penetrating by a teeny bit, extra impulse is applied. This would result in unnecessary jitter and objects will hardly sit tight when they are supposed to be at rest.

The condition can be greatly improved if we allow objects to penetrate a bit before actually applying Baumgarte Stabiliation. Recall that the Baumgarte term within the bias term of the contact constraint equation is:

where is the penetration depth.

Continue reading →

This post is part of my Game Physics Series.

Contact constraints are amongst the most important constraints for a physics engine, because you would want to resolve collision in most scenarios. And if not done properly, your rigid bodies can behave in a very visually jarring way to the player.

Derivation

Remember that Sequential Impulse models constraints in the form of , where is the Jacobian matrix, is the velocity vector, and is the bias term. Erin Catto (author of Box2D) proposed a systematic way to derive velocity constraints: you first find the position constraint , and then differentiate it with respect to time to obtain the velocity constraint . Sometimes, it is more intuitive to directly derive the velocity constraint itself, and I think it is the case for contact constraints. However, for the purpose of demonstration, I will first find the equation for the position constraint, and then derive the velocity constraint.

Based on the contact format previously described, a possible interface for contact data may look as follows.

struct Contact
{
  // contact point data
  Vec3 globalPositionA;
  Vec3 globalPositionB;
  Vec3 localPositionA;
  Vec3 localPositionB;
 
  // these 3 vectors form an orthonormal basis
  Vec3 normal; // points from colliderA to colliderB
  Vec3 tangent1, tangent2;
 
  // penetration depth
  float depth; 
 
  // for clamping (more on this later)
  float normalImpulseSum;
  float tangentImpulseSum1;
  float tangentImpulseSUm2;
 
  Contact(void)
    : normalImpulseSum(0.0f)
    , tangentImpulseSum1(0.0f)
    , tangentImpulseSum2(0.0f)
  { }
 
  // there's typically more stuff
  // but omitted for simplicity's sake
};

Let us look at the figure below before moving onto finding the position constraint.

Continue reading →

This post is part of my Game Physics Series.

Constraints

The resolution phase of a constraints-based physics engine uses the concept of constraints. A free rigid body in 3D has 6 degrees of freedom: 3 positional and 3 rotational; a rigid body in 2D has 3 degrees of freedom: 2 positional and 1 rotational. A constraint decreases the degrees of freedom of a rigid body. For instance, a constraint that pins an object in space at its center of mass decreases the object’s degrees of freedom by 3: all the positional degrees of freedom are removed and the object can thus now only rotate with 3 degrees of freedom.

In a constraint-based physics engine, we model everything as a constraint: including collision contacts, frictions, springs, pulleys, you name it. A joint is a constraint that involves the interaction of 2 rigid bodies; the examples enumerated here are all technically joints.

Mathematically, a constraint is of the form , where is the expression representing the constraint. We would specifically express as a linear combination of positional properties (linear position and angular position, a.k.a. orientation); for joints, would contain positional properties from both rigid bodies.

Continue reading →

This post is part of my Game Physics Series.

Contact Data

GJK tells us whether two colliders are colliding and nothing more. In order to correctly resolve collision, we would need to generate contacts. As mentioned earlier, contacts are approximation of the touching region of two colliding shapes, and the collection of contacts between two colliders are collectively called a contact manifold.

A typical piece of contact data contains the following information:

• Two contact points in world space, each representing the deepest penetrating point of one collider. (positions x2)
• Two contact points in local spaces of individual colliders, each corresponding to a contact point in world space. This information is crucial for maintaining persistent contacts. (positions x2)
• Contact normal representing the “best direction” to separate the two colliding colliders. (vector x1)
• Two contact tangents perpendicular to each other and the contact normal. These vectors are used to resolve the frictional part of collision resolution. (vectors x2)
• Penetration depth, a scalar value that represents how deep the overlap of the two colliders is. (float x1)

Continue reading →

This post is part of my Game Physics Series.

As mentioned earlier, all collision detection algorithms are essentially determining if the CSO of two shapes contains the origin. The collision detection I am going to introduce to you here, the Gilbert-Johnson-Keerthi (GJK) algorithm, is no different.

GJK is one of the most popular collision detection algorithms, because it is very efficient and intuitive (once you get it, of course). It basically attempts to find a subset, or a “simplex” to be precise, of the CSO that contains the origin. A simplex in n-dimension, by definition, is a minimal geometry in n-dimension that can be tightly tiled to fill up the space; for instance, a triangle is a 2D simplex, and tetrahedron is a 3D simplex. Inside the CSO of two colliding shapes, we can find a point (0D simplex), a line (1D simplex), a triangle (2D simplex), or a tetrahedron (3D simplex) that contains the origin.

Continue reading →

This post is part of my Game Physics Series.

Configuration Space Object (CSO), a.k.a. Minkowski Difference or Minkowski Configuration Object, is a very important concept for collision detection. In addition to CSO, support function is an equally important mathematical concept & tool. Many algorithms related to collision detection, including the Gilbert-Johnson-Keerthi (GJK) algorithm, Expanding Polytop Algorithm (EPA), and Minkowski Portal Refinement (MPR) algorithm, heavily depend on the concept of CSO and the use of support functions.

Configuration Space Object

As complicated as its name sounds, it is actually a very simple concept. Let’s first look at a mathematical operation called the Minkowski Sum.

Let and be two shapes (2D or 3D), the Minkowski Sum of and , denoted , is a shape resulted from “sweeping” all across the region occupied by , or sweeping across (the result is the same). Another way of saying this is that the Minkowski Sum of and is a shape that is a collection of points, where each point is the result of a point from plus a point from .

Let’s look at something more visual. The Minkowski Sum of a circle and a rectangle is a rounded rectangle.

Continue reading →