This post is part of my Game Math Series.
Source files are on GitHub
Check out this post if you want to see more visual examples of numeric springing.
Numeric springing is a very powerful tool for procedural animation. You specify the initial value, initial velocity, target value, and some spring-related parameters; the result is a smooth springing effect. You can apply this technique to all sorts of numeric properties, some common ones being position, rotation, and scale of an object.

The Common But Designer-Unfriendly Way
Here is a common, yet designer-unfriendly, implementation of numeric springing. Let ![]() and
and ![]() denote the numeric value and velocity, respectively, at frame
denote the numeric value and velocity, respectively, at frame ![]() ; and let
; and let ![]() ,
, ![]() ,
, ![]() ,
, ![]() , denote the spring stiffness, damping factor, time step between frames, and target value, respectively.
, denote the spring stiffness, damping factor, time step between frames, and target value, respectively.
![]()
Let’s dissect this implementation.
The difference between the target value and the current value ![]() contributes to the velocity change after multiplied by the spring stiffness
contributes to the velocity change after multiplied by the spring stiffness ![]() . The larger the difference and spring stiffness, the larger the change in velocity.
. The larger the difference and spring stiffness, the larger the change in velocity.
The new velocity ![]() inherits the value from the old velocity
inherits the value from the old velocity ![]() scaled by the damping factor
scaled by the damping factor ![]() , which should be a value between zero and one. If the damping factor is equal to one, then no scaling happens, and the new velocity completely inherits the value from the old velocity. If the damping factor is a fraction of one, then the magnitude of oscillation will decrease gradually.
, which should be a value between zero and one. If the damping factor is equal to one, then no scaling happens, and the new velocity completely inherits the value from the old velocity. If the damping factor is a fraction of one, then the magnitude of oscillation will decrease gradually.
That seems all reasonable and good, but just what exactly are the values for ![]() and
and ![]() do we need to achieve a specific springing effect, say an oscillation at 5Hz frequency and the oscillation magnitude decreases by 90% every one second? Many people just decide to bite the bullet and spend a large amount of time hand-tweaking the values for
do we need to achieve a specific springing effect, say an oscillation at 5Hz frequency and the oscillation magnitude decreases by 90% every one second? Many people just decide to bite the bullet and spend a large amount of time hand-tweaking the values for ![]() and
and ![]() , until the result is acceptably close to the desired effect.
, until the result is acceptably close to the desired effect.
We Can Be Exact
Now let’s take a look at the differential equation for a damped spring system centered around ![]() .
.
![]()
I won’t go into details as to how this equation is derived. All you really need to know is that ![]() (omega) and
(omega) and ![]() (zeta) govern how the system behaves and what they mean.
(zeta) govern how the system behaves and what they mean.
![]() is the angular frequency of the oscillation. An angular frequency of
is the angular frequency of the oscillation. An angular frequency of ![]() (radians per second) means the oscillation completes one full period over one second, i.e. 1Hz.
(radians per second) means the oscillation completes one full period over one second, i.e. 1Hz.
![]() is the damping ratio. A damping ratio of zero means there is no damping at all, and the oscillation just continues indefinitely. A damping ratio between zero and one means the spring system is underdamped; oscillation happens, and the magnitude of oscillation decreases exponentially over time. A damping ratio of 1 signifies a critically damped system, where this is the point the system stops showing oscillation, but only converging to the target value exponentially. Any damping ratio above 1 means the system is overdamped, and the effect of springing becomes more draggy as the damping ratio increases.
is the damping ratio. A damping ratio of zero means there is no damping at all, and the oscillation just continues indefinitely. A damping ratio between zero and one means the spring system is underdamped; oscillation happens, and the magnitude of oscillation decreases exponentially over time. A damping ratio of 1 signifies a critically damped system, where this is the point the system stops showing oscillation, but only converging to the target value exponentially. Any damping ratio above 1 means the system is overdamped, and the effect of springing becomes more draggy as the damping ratio increases.
Here’s a figure I borrowed form Erin Catto‘s presentation on soft constraints, to show you the comparison of undamped, underdamped, critically damped, and overdamped systems.
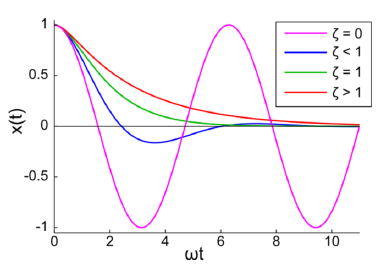
Below are the equations for simulating a damped spring system using the implicit Euler method.
![]()
Solving ![]() and
and ![]() in terms of
in terms of ![]() and
and ![]() using Cramer’s rule, we get:
using Cramer’s rule, we get:
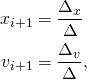
where:
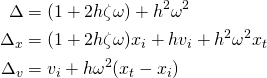
Below is a sample implementation in C++. The variables x and v are initialized once and then passed into the function by reference every frame, where the function keeps updating their values every time it’s called.
/*
x - value (input/output)
v - velocity (input/output)
xt - target value (input)
zeta - damping ratio (input)
omega - angular frequency (input)
h - time step (input)
*/
void Spring
(
float &x, float &v, float xt,
float zeta, float omega, float h
)
{
const float f = 1.0f + 2.0f * h * zeta * omega;
const float oo = omega * omega;
const float hoo = h * oo;
const float hhoo = h * hoo;
const float detInv = 1.0f / (f + hhoo);
const float detX = f * x + h * v + hhoo * xt;
const float detV = v + hoo * (xt - x);
x = detX * detInv;
v = detV * detInv;
}
Designer-Friendly Parameters
Now we have our formula and implementation all worked out, what parameters should we expose to the designers from our spring system so that they can easily tweak the system?
Inspired by the aforementioned presentation by Erin Catto, I propose exposing the oscillation frequency ![]() in Hz, and the fraction of oscillation magnitude reduced
in Hz, and the fraction of oscillation magnitude reduced ![]() over a specific duration
over a specific duration ![]() due to damping.
due to damping.
Mapping ![]() to
to ![]() is easy, you just multiply it by
is easy, you just multiply it by ![]() :
:
![]()
Mapping ![]() and
and ![]() to
to ![]() is a little bit more tricky.
is a little bit more tricky.
First you need to understand that the oscillation magnitude decreases exponentially with this curve:
![]()
After plugging in ![]() and
and ![]() , we get:
, we get:
![]()
So we can solve for ![]() :
:
![]()
For example, if we want the oscillation to decrease by 90% (![]() ) every 0.5 second (
) every 0.5 second (![]() ) with oscillation frequency 2Hz (
) with oscillation frequency 2Hz (![]() ), then we get:
), then we get:
![]()
Conclusion
Numeric springing is a very powerful tool for procedural animation, and now you know how to precisely control it. Given the desired oscillation frequency and percentage of oscillation magnitude reduction over a specific duration, you can now compute the exact angular frequency ![]() and damping ratio
and damping ratio ![]() necessary to create the desired springing effect.
necessary to create the desired springing effect.
By the way, let’s look at the animated example shown above again:

This animation was created with ![]() (4 full oscillation periods per second) and
(4 full oscillation periods per second) and ![]() (oscillation magnitude decreases by 99.7% every second).
(oscillation magnitude decreases by 99.7% every second).


Hey Allen, thanks for writing this article. It’s leads helping the tweens in my game. One suggestion: the code snippet having abbreviated argument names like x, v, xt, etc made the article and especially the spring function much harder to parse. I think it would help new readers understand quickly if those function had full names.
Thanks for the feedback. I’m glad you find it helpful.
And yes, I did consider using variable names that are more descriptive; however, I decided that it’s more important to have the code nicely formatted without line-wrapping in the blog post, so I kept the variable names short. I think the comments above the function explaining the variables should be enough.
Pingback: Precise Control over Numeric Springing |
Hi Allen, thanks for the post! I just wanted to add one cent to this. If the oscillator has a maximum amplitude of M at start t=0 (in the post M=1), then we just need to multiply Pd by M.
Can you explain? I thought Pd already specifies the percentage of reduction (regardless of M), so M is reduced to Pd * M after duration td. Or am I missing something?
What I meant is that in the post |x(0)| = 1, but what if I want |x(0)| = M, then |x(td)| = Pd*M. However, now that I think more about it, it is better to leave x(t) to be in [-1,1] as it is in your post, and use its value to whatever amplitude we need outside (just like we do with easing functions). Sorry for the confusion :/
Actually, it’s only the figure that says |x(0)| = 1. The equations I showed don’t require |x(0)| = 1. Perhaps I should have clarified that.
wait, but we have explicitly x(t) = exp(-zwt), and from here we have x(t=0) = exp(0) = 1 , or am I missing something?
Yeah. That’s a typo. I meant to write y(t) = exp(-zwt), representing the oscillation reduction percentage (fixed now).