原始檔案與未來教學更新資訊可於Patreon取得
您可於Twitter上追蹤我
本文屬於遊戲數學系列文
Here is the original English post.
本文之英文原文在此
前備教學
大綱
在上個教學中,我們認識到了兩個基礎三角函數:正弦與餘弦。這次我們要來學習第三個基礎三角函數:正切(tangent)。這三者為三角函數的根基,能夠用來解決遊戲開發過程中會遇到的各種問題。
你將可透過本教學學會:
- 正切函數的幾何意義
- 正弦函數、餘弦函數、與正切函數之間的關係
- 如何用正切函數做出圓滑的入場與退場效果
- 三角形的邊與三角函數之間的關係
- 給定初速與仰角,如何模擬砲彈路徑
- 在發射砲彈前,如何預測砲彈路徑
- 給定水平距離和仰角,如何定位砲彈的目標

正切函數的幾何意義
我們先來看看上個教學中的單位圓,圓上有一點![]() ,X軸(+X方向)與連接
,X軸(+X方向)與連接![]() 與原點的線段之間的夾角為
與原點的線段之間的夾角為![]() 。
。
從上個教學中已經得知![]() 的座標
的座標![]() ,我們現在來看看一個新的三角函數:正切(
,我們現在來看看一個新的三角函數:正切(![]() – 念作”tangent of theta”)。它是連接
– 念作”tangent of theta”)。它是連接![]() 與原點的線段的斜率。
與原點的線段的斜率。
一條線的斜率是其垂直變動與水平變動之間的比率。舉例來說,我們來看看以下線段:
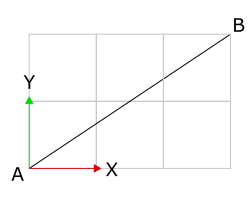
從點![]() 移動到點
移動到點![]() ,往+X方向移動3單位,並往+Y方向移動2單位,所以此線段的斜率是
,往+X方向移動3單位,並往+Y方向移動2單位,所以此線段的斜率是![]() 。
。
至於如以下這個”走下坡”的線段:
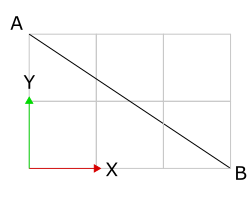
其斜率則為![]() ,因為垂直移動與水平移動的比率為負數,斜率便為負數。
,因為垂直移動與水平移動的比率為負數,斜率便為負數。
現在,回到之前的單位圓圖:
我們看到從原點往![]() 直線移動,會水平移動
直線移動,會水平移動![]() 距離並且垂直移動
距離並且垂直移動![]() 距離,所以連接
距離,所以連接![]() 與原點的線段斜率為
與原點的線段斜率為![]() 。於是
。於是![]() .
.
但那只是個數學式子而已,我們來看看![]() 與單位圓的關係到底是如何。首先,於
與單位圓的關係到底是如何。首先,於![]() 畫個單位圓的切線,也就是一條通過
畫個單位圓的切線,也就是一條通過![]() 且與連接
且與連接![]() 與圓點的線段垂直的直線。
與圓點的線段垂直的直線。
現在只看該切線介於![]() 與X軸的部分,並且標記一些點:
與X軸的部分,並且標記一些點:
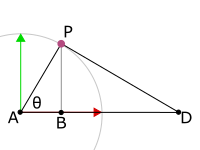
![]() 與
與![]() 為直角,然後
為直角,然後 ![]() ,並且令
,並且令![]() 表示連接兩點
表示連接兩點![]() 與
與![]() 的線段長度。
的線段長度。
接下來,將上圖拆成以下兩個直角三角形:

三角形的內角和為![]() ,而且兩個三角形分別已經有兩個角為
,而且兩個三角形分別已經有兩個角為![]() 和
和![]() ,沒有被標記的角(
,沒有被標記的角(![]() 和
和![]() )便是相同的:
)便是相同的: ![]() 。
。
當兩個三角形各自的三個角度組合相同,他們便互相為相似三角形。意即若將其中一個三角形等比例縮放、旋轉、與翻轉,就有辦法變成跟另外一個三角形一模一樣。
兩個三角形互相為相似三角形時,其中一個三角形的任意兩邊長度比例將會等同於另外一個三角形的對應兩邊長度比例,於是:
![]()
已知![]() 的座標為
的座標為![]() ,於是
,於是![]() 且
且![]() 。然後
。然後 ![]() 為單位圓的半徑,於是
為單位圓的半徑,於是![]() ,便可將上面的等式轉換成:
,便可將上面的等式轉換成:
![]()
我們也知道![]() ,於是等式最後會變成:
,於是等式最後會變成:
![]()
我們找到![]() 的幾何意義了!
的幾何意義了!
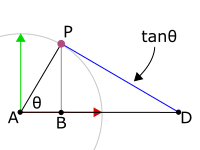
![]() 的絕對值等同於通過
的絕對值等同於通過![]() 、介於
、介於![]() 與X軸之間的切線線段長度。注意到我使用絕對值這個字眼,因為
與X軸之間的切線線段長度。注意到我使用絕對值這個字眼,因為![]() 的正負號是根據
的正負號是根據![]() 與
與![]() 的正負號來決定。以下插圖將等同於
的正負號來決定。以下插圖將等同於![]() 絕對值的切線線段以藍色標記:
絕對值的切線線段以藍色標記:
正切曲線
我們已經在上個教學中看過![]() 和
和![]() 針對
針對![]() 的作圖,兩者重疊在一起看起來如下:
的作圖,兩者重疊在一起看起來如下:
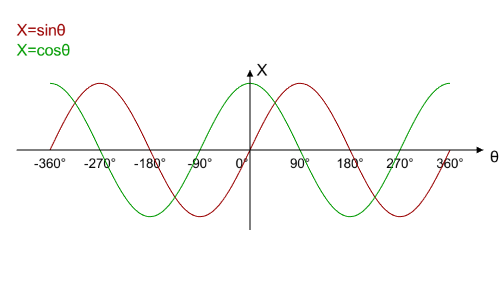
現在再把![]() 重疊上去:
重疊上去:
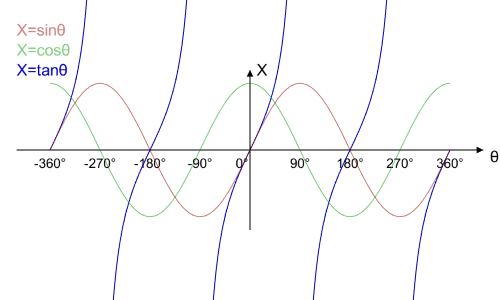
請留意![]() 不像
不像![]() 與
與![]() ,其值沒有受限於
,其值沒有受限於![]() 範圍內。因為
範圍內。因為![]() ,當
,當![]() 接近0的時候,
接近0的時候,![]() 的絕對值則會趨近於無限大。同時也請留意
的絕對值則會趨近於無限大。同時也請留意![]() 的週期為
的週期為![]() ,不同於
,不同於![]() 與
與![]() 的週期
的週期![]() 。
。
另一值得關注的一點,是此三個函數之間正負號的相互關係。因為![]() ,當
,當![]() 與
與![]() 正負號相同的時候
正負號相同的時候![]() 為正值,反之則為負值。
為正值,反之則為負值。
現在,來試試看把物件的X座標設成正切函數值:
float tan = Mathf.Tan(Rate * Time.time); obj.transform.position = Vector3(tan, 0.0f, 0.0f);
物件從-X方向高速入場、減速、然後又加速往+X方向退場。
我們可以利用這個特性來製作如下的流星效果:
float tan = Mathf.Tan(Rate * Time.time); obj.transform.position = center + moveDirection * tan;
加減速的效果似乎沒有很明顯,那來試著使用![]() 的三次方將加減速效果放大:
的三次方將加減速效果放大:
float tan = Mathf.Tan(Rate * Time.time); float tan3 = tan * tan * tan; obj.transform.position = center + moveDirection * tan3;
三角函數、角度、與三角形
瞭解了三個基礎三角函數與單位圓的關係之後,,讓我們來探討它們與直角三角形的關係。畢竟這些函數被稱作三角函數,與三角形是關係密切的。
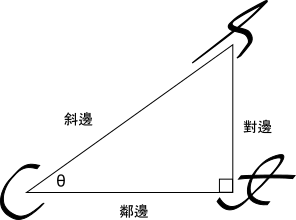
首先,先介紹一些術語,以下是個一角大小為![]() 的直角三角形:
的直角三角形:
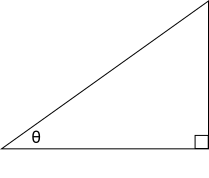
兩端為角![]() 與直角的邊稱作鄰邊(adjacent side),因為緊鄰
與直角的邊稱作鄰邊(adjacent side),因為緊鄰![]() 。另一與直角相鄰的邊稱作對邊(opposite side),因為位於
。另一與直角相鄰的邊稱作對邊(opposite side),因為位於![]() 對面。剩下最長且位於直角對面的一邊則為斜邊(hypotenuse)。
對面。剩下最長且位於直角對面的一邊則為斜邊(hypotenuse)。
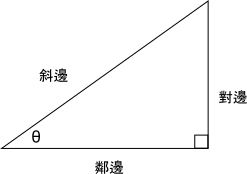
以下為三個基礎三角函數與這些邊長的關係:

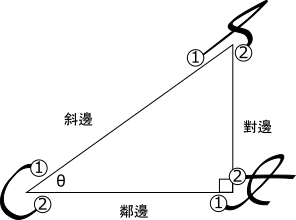
一時無法記住這些關係的話,可以參考這個視覺記憶法。將![]() 、
、![]() 、和
、和![]() 三者個首字母用草寫如此書寫在三角形的周圍(請原諒我難看的手寫):
三者個首字母用草寫如此書寫在三角形的周圍(請原諒我難看的手寫):
書寫一個字母的時候,其對應的函數即為”第一個擦過的邊分之第二個擦過的邊“:
再來看一次算式:
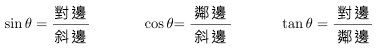
不管此直角三角形的大小為何,這些等式恆成立,因為三角形兩邊之比例與各邊的絕對長度是無關的。
若將直角三角形等比例縮放,大小調整為斜邊長度剛好是1,便可把這個直角三角形放入單位圓中,並且與圓周上的一點![]() 一起比較:
一起比較:
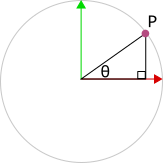
可以發現上述三角函數等式與![]() 的座標
的座標![]() 是相容的:
是相容的:
![]()
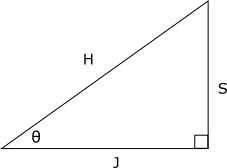
知道了三角函數與直角三角形邊長之間的關係之後,若碰到一角大小為![]() 的直角三角形,且知道其中一邊的邊長,便可用三角函數表達另外兩邊的長度。
的直角三角形,且知道其中一邊的邊長,便可用三角函數表達另外兩邊的長度。
讓我們用![]() 代表鄰邊(adjacent side)長度,
代表鄰邊(adjacent side)長度,![]() 代表對邊(opposite side)長度,
代表對邊(opposite side)長度,![]() 代表斜邊(hypotenuse)長度:
代表斜邊(hypotenuse)長度:
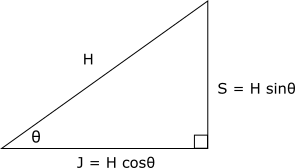
若已知斜邊長度![]() ,則鄰邊長度
,則鄰邊長度![]() ,對邊長度
,對邊長度![]() :
:
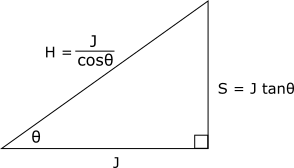
若已知鄰邊長度![]() ,則對邊長度
,則對邊長度![]() ,斜邊長度
,斜邊長度![]() :
:
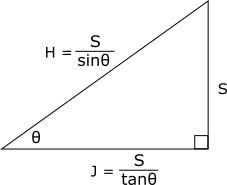
若已知對邊長度![]() ,則鄰邊長度
,則鄰邊長度![]() ,對邊長度
,對邊長度![]() :
:
模擬與預測砲彈路徑
終於到實戰範例的時候了!讓我們來看看,當給定砲彈發射初始速率、發射水平角、與發射仰角,要如何模擬砲彈的行徑,甚至是如何在發射前就預測好完整路徑。
在這之前,先快速地把動力學的專有名詞複習一下。物件在空間中的定位稱為位置(position),物件的位置隨時間之改變率稱為速度(velocity – 通常表達為每秒之位置變化),物件的速度向量長度為速率(speed),物件的速度隨時間之改變率稱為加速度(acceleration – 通常表達為每秒之速度變化)。
尤拉方法(Euler Method)是個可以用來模擬物件移動的簡易演算法:針對每個可移動的物件,隨其位置同時保存速度資料。每一次更新(update) – 又稱時間推進(time step),對物件的速度加上加速度乘以delta time (兩次更新之間的時間差)之變化量,在對物件的位置加上速度乘以delta time之變化量:
velocity += acceleration * deltaTime; position += velocity * deltaTime;
欲模擬大約位於地面高度且人體尺寸附近的重力,我們使用一個長度固定且方向往下的向量。以下這個範例使用尤拉方法,模擬一個初始速度向右上方的2D物件行進路線:
若我們在一禎(frame)當中進行多次時間推進,而每過幾次推進便繪製一個小點,就可以畫出物件路徑的預測圖:
velocity = initialVelocity;
position = initialPosition;
for (int i = 0; i < NumIterations; ++i)
{
velocity += acceleration * deltaTime;
position += velocity * deltaTime;
if (i % IterationsPerDot != 0)
continue;
DrawDot(position);
}
現在,令砲彈初始速率(初始速度向量的長度)為![]() ,發射水平角大小為
,發射水平角大小為![]() ,發射仰角為
,發射仰角為![]() (phi)。令
(phi)。令![]() 方向為大砲的前方,
方向為大砲的前方,![]() 方向為大砲的右方(Unityg使用左手座標系)。
方向為大砲的右方(Unityg使用左手座標系)。
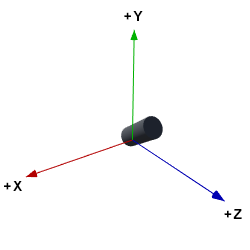
欲計算初始速度,我們需要先計算出相同方向的單位向量(長度為1之向量),並將其長度乘以![]() 。
。
下圖顯示![]() 方向的單位向量(紅色)、
方向的單位向量(紅色)、![]() 方向的單位向量(綠色)、
方向的單位向量(綠色)、![]() 方向的單位向量(藍色)、初始速度方向的單位向量(黑色並標記為
方向的單位向量(藍色)、初始速度方向的單位向量(黑色並標記為![]() )、初始速度水平分量同向的單位向量(灰色並標記為
)、初始速度水平分量同向的單位向量(灰色並標記為![]() )、砲彈發射水平角
)、砲彈發射水平角![]() (介於
(介於![]() 與
與![]() 之間)、與發射仰角
之間)、與發射仰角![]() (介於
(介於![]() 與
與![]() 之間):
之間):
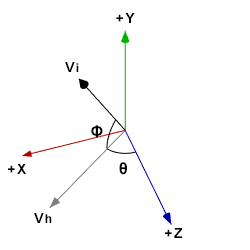
目標是要找出![]() 並且將其乘上
並且將其乘上![]() ,我們可以先把上圖拆成兩個各自含有單位圓的圖。
,我們可以先把上圖拆成兩個各自含有單位圓的圖。
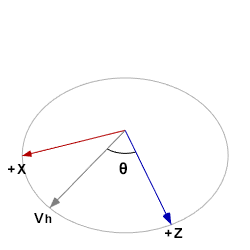
首先是個水平單位圓圖,含有![]() 、
、![]() 、
、![]() 、和
、和![]() :
:
再來是個垂直單位圓圖,含有![]() 、
、![]() 、
、![]() 、和
、和![]() :
:

調整觀看第一個水平單位原圖的角度,找出能夠看到這個令人熟悉的單位圓圖:
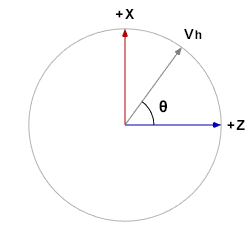
我們之前已經看過這個算法了,![]() 與
與![]() 平行的分量大小為
平行的分量大小為![]() ,與
,與![]() 平行的分量大小則為
平行的分量大小則為![]() ,於是我們便能算出
,於是我們便能算出![]() 。
。
用同樣的視角觀看第二個垂直的單位圓圖:
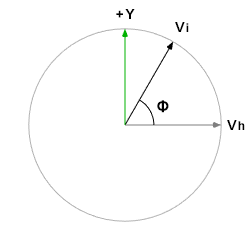
同樣的算法,![]() 與
與![]() 平行的分量大小為
平行的分量大小為![]() ,與
,與![]() 平行的分量大小則為
平行的分量大小則為![]() ,於是我們可以算出
,於是我們可以算出![]() :
:
![]()
將![]() 乘上
乘上![]() 便是我們所要找的初始速度向量:
便是我們所要找的初始速度向量:
![]()
其對應的程式碼如下:
Vector3 ComputeInitialVelocity()
{
float sinTheta = Mathf.Sin(HorizontalAngle);
float cosTheta = Mathf.Cos(HorizontalAngle);
float sinPhi = Mathf.Sin(ElevationAngle);
float cosPhi = Mathf.Cos(ElevationAngle);
return
InitialSpeed
* new Vector3
(
cosPhi * sinTheta,
sinPhi,
cosPhi * cosTheta
);
}
給定初始速率、水平角、和仰角,能夠算出砲彈發射的初始速度向量,我們便能模擬與預測砲彈路徑:
void FireCannon()
{
velocity = ComputeInitialVelocity();
obj.transform.position = InitialPosition;
}
void Update()
{
float dt = Time.deltaTime;
velocity += acceleration * dt;
obj.transform.position += velocity * dt;
}
void DrawTrajectory()
{
float dt = Time.fixedDeltaTime;
Vector3 velocity = ComputeInitialVelocity();
Vector3 position = InitialPosition;
for (int i = 0; i < NumIterations; ++i)
{
velocity += acceleration * dt;
position += velocity * dt;
if (i % IterationsPerDot != 0)
continue;
DrawDot(position);
}
放置砲彈目標
我們能夠發射砲彈了,現在來放置一些目標吧。給定相對於大砲的水平距離與仰角,要如何在正確的位置放置目標?下圖是欲達到的結果,每個目標與大砲的水平(XZ平面上)距離相同,並且水平間隔相等,也就是相對於大砲的水平角間距相等。

我們已經知道水平角為![]() 時,可以求得水平單位向量
時,可以求得水平單位向量![]() ,將其與給定的水平距離(標記為
,將其與給定的水平距離(標記為![]() )相乘,便可得到目標對於大砲的相對水平位移
)相乘,便可得到目標對於大砲的相對水平位移![]() 。將
。將![]() 等值相隔,便可得到各目標的XZ座標(下圖中的紅點):
等值相隔,便可得到各目標的XZ座標(下圖中的紅點):

最後一步是求得各目標的Y座標,也就是離地距離。先前已經看過,一個角大小為![]() 的直角三角形,若其鄰邊長度為
的直角三角形,若其鄰邊長度為![]() ,則其對邊長度為
,則其對邊長度為![]() 。
。

將![]() 替換為水平距離
替換為水平距離![]() ,
,![]() 替換為仰角
替換為仰角![]() ,則可求得各目標的Y座標值為
,則可求得各目標的Y座標值為![]() 。
。

我們終於能將目標放置在正確的位置了:
float theta = -0.5f * AngleInterval * (NumTargets - 1);
float elevationTan = Mathf.Tan(ElevationAngle);
foreach (var target in targetArray)
{
Vector3 horizontalVec =
HorizontalDistance
* new Vector3
(
Mathf.Sin(theta),
0.0f,
Mathf.Cos(theta)
);
theta += AngleInterval;
Vector3 verticalVec =
HorizontalDistance
* elevationTan
* Vector3.up;
target.transform.position =
Cannon.position
+ horizontalVec
+ verticalVec;
}

我們還沒有討論要如何偵測砲彈是否與目標碰撞,所以砲彈目前會穿過目標:
碰撞偵測(collision detection)非本教學的主題,所以我就很快地帶過球與球之間地碰撞偵測方法。要偵測兩球是否碰撞,就檢查兩球心連線長度是否小於兩球半徑和。若砲彈與目標碰撞,我們便將兩者摧毀。
Vector3 cannonballToTargetVec =
target.transform.position
- cannonball.transform.position;
float cannonballToTargetDist = cannonballToTargetVec.magnitude;
if (cannonballToTargetDist < cannonballRadius + targetRadius)
{
DestroyCannonball();
DestroyTarget();
}
用同樣的方法,我們可以偵測砲彈預測路徑與目標碰撞,提早中止路徑繪製。
然而,這個方法是離散(discrete)碰撞偵測,意即當砲彈行進速率夠大時,還是會穿過目標。我們可以用連續(continuous)碰撞偵測技巧來解決此問題,但這同樣也不是本教學的範疇,我會在未來的教學中再對其詳加介紹。
總結
我們在上個教學中認識了兩個基礎三角函數:正弦與餘弦。於本教學中,我們看到了第三個基礎三角函數 – 正切 – 的幾何意義。我們也學會了正弦、餘弦、與正切對單位圓與直角三角形的關係。
接著,我們將正切函數對角度的作圖與正弦和餘弦的作圖重疊。現在也有能力用正切函數製作圓滑的物件入場與退場效果。
最後,我們學會了當給定初始速率、水平角、和仰角,如何用三個基礎三角函數模擬與預測發射砲彈的路徑。我們也學會了給定相對於大砲的水平距離和仰角,如何放置砲彈目標。
現在我們習得了解決日常遊戲開發問題所必備的三個基礎三角函數。於未來的教學中,我將介紹更多以這些三角函數為基底而衍伸的數學工具,並且會展示其能套用到的實務範例。
若您喜歡這篇教學,請考慮到Patreon支持我。感謝!

