This post is part of my Game Math Series.
Also, this post is part 2 of a series (part 1) leading up to a geometric interpretation of Fourier transform and spherical harmonics.
Drawing analogy from vector projection, we have seen what it means to “project” a curve onto another in the previous post. This time, we’ll see how to find a the closest vector on a plane via vector projection, and then we’ll see how it translates to finding the best approximation of a curve via curve “projection”. This handy analogy can help us take another step closer to a geometric interpretation of Fourier transform and spherical harmonics later.
Closest Vector on a Plane
Given vectors ![]() ,
, ![]() , and
, and ![]() , the closest vector on the plane formed (or “spanned” in linear algebra jargon) by
, the closest vector on the plane formed (or “spanned” in linear algebra jargon) by ![]() and
and ![]() is the projection of
is the projection of ![]() onto the plane. This projection, denoted
onto the plane. This projection, denoted ![]() , is a combination of scaled
, is a combination of scaled ![]() and
and ![]() , in the form of
, in the form of ![]() , that has the least error from
, that has the least error from ![]() .
.
The error is measured by the magnitude of the difference vector:
![]()
As pointed out in the previous post, minimizing this error is essentially equivalent to minimizing the root mean square error (RMSE):
![]()
This is what the relationship of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() looks like visually:
looks like visually:
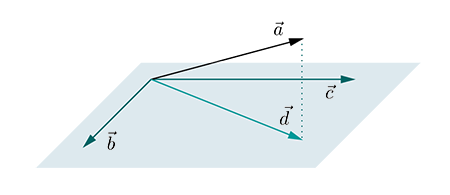
The projection of ![]() onto the plane spanned by
onto the plane spanned by ![]() and
and ![]() , is the vector
, is the vector ![]() on the plan that has the least error from
on the plan that has the least error from ![]() , and the difference vector
, and the difference vector ![]() is orthogonal to the plane.
is orthogonal to the plane.
So how do we compute ![]() ? In the previous post we’ve seen how to project a vector onto another, so would computing
? In the previous post we’ve seen how to project a vector onto another, so would computing ![]() be as simple as projecting
be as simple as projecting ![]() onto
onto ![]() , and then project the result again onto
, and then project the result again onto ![]() ? Not really. Here’s why:
? Not really. Here’s why:
As you can see in the figure above, ![]() isn’t parallel to
isn’t parallel to ![]() nor
nor ![]() . Projecting
. Projecting ![]() onto
onto ![]() would give you a vector that is parallel to
would give you a vector that is parallel to ![]() , and a subsequent projection onto
, and a subsequent projection onto ![]() would leave you with a result that is parallel to
would leave you with a result that is parallel to ![]() , which is definitely not
, which is definitely not ![]() .
.
One way to do it is to calculate a vector orthogonal to the plane, i.e. a plane normal ![]() , by taking the cross product of the two vectors that span the plane:
, by taking the cross product of the two vectors that span the plane: ![]() . Then, take out the part in
. Then, take out the part in ![]() that is parallel to
that is parallel to ![]() by subtracting the projection of
by subtracting the projection of ![]() onto
onto ![]() from
from ![]() . What is left of
. What is left of ![]() is the part of
is the part of ![]() that is parallel to the plane, i.e. the projection:
that is parallel to the plane, i.e. the projection:
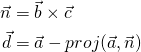
But, I want to talk about another way of performing the projection, which is easier to translate to curves later. ![]() and
and ![]() are not necessarily orthogonal to each other. Let’s find two orthogonal vectors that lie on the plane spanned by
are not necessarily orthogonal to each other. Let’s find two orthogonal vectors that lie on the plane spanned by ![]() and
and ![]() . Then, we split
. Then, we split ![]() into two parts, one parallel to one vector and one parallel to the other vector. Finally, we combine these two parts together to obtain a vector that is essentially the part of
into two parts, one parallel to one vector and one parallel to the other vector. Finally, we combine these two parts together to obtain a vector that is essentially the part of ![]() that is parallel to the plane.
that is parallel to the plane.
As a simple illustration, if the plane is the X-Z plane, then the obvious two orthogonal vectors of choice would be ![]() and
and ![]() . To project a vector
. To project a vector ![]() onto the X-Z plane, we split it into a part that is parallel to
onto the X-Z plane, we split it into a part that is parallel to ![]() , which is
, which is ![]() , and a part that is parallel to
, and a part that is parallel to ![]() , which is
, which is ![]() . Combining those two parts together would give us
. Combining those two parts together would give us ![]() . This makes sense, because projecting a vector onto the X-Z plane is just as simple as dropping the Y component.
. This makes sense, because projecting a vector onto the X-Z plane is just as simple as dropping the Y component.
Now, given two arbitrary vectors ![]() and
and ![]() that span a plane, we can generate two orthogonal vectors, denoted
that span a plane, we can generate two orthogonal vectors, denoted ![]() and
and ![]() , by using a method called the Gram-Schmidt process. The first vector
, by using a method called the Gram-Schmidt process. The first vector ![]() would simply be the
would simply be the ![]() . To compute the second vector
. To compute the second vector ![]() , we take away from
, we take away from ![]() its part that is parallel to
its part that is parallel to ![]() ; what’s left of
; what’s left of ![]() is orthogonal to
is orthogonal to ![]() :
:
![]()
To compute ![]() , we combine the parts of
, we combine the parts of ![]() that are parallel to
that are parallel to ![]() and
and ![]() , respectively:
, respectively:
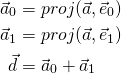
More on Gram-Schmidt Process
The Gram-Schmidt process is actually more general than described above. It can apply to higher dimensions. Given ![]() vectors, denoted
vectors, denoted ![]() to
to ![]() , in an
, in an ![]() -dimensional space (
-dimensional space (![]() ), and if the
), and if the ![]() vectors are linearly independent, i.e. they span an
vectors are linearly independent, i.e. they span an ![]() -dimensional subspace, then we can generate
-dimensional subspace, then we can generate ![]() vectors that are orthogonal to each other, denoted
vectors that are orthogonal to each other, denoted ![]() through
through ![]() , spanning the same subspace, using the Gram-Schmidt process.
, spanning the same subspace, using the Gram-Schmidt process.
The first vector ![]() would simply be
would simply be ![]() . To compute the second vector
. To compute the second vector ![]() , we take away from
, we take away from ![]() its part that is parallel to
its part that is parallel to ![]() . To compute the third vector
. To compute the third vector ![]() , we take away from
, we take away from ![]() its part that is parallel to all previously generated orthogonal vectors,
its part that is parallel to all previously generated orthogonal vectors, ![]() and
and ![]() . Repeat this process until we have reached
. Repeat this process until we have reached ![]() and produced
and produced ![]() :
:
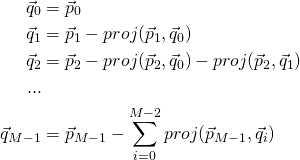
Projecting an ![]() -dimensional vector onto this
-dimensional vector onto this ![]() -dimensional subspace would involve combining the parts of the vector parallel to each of the orthogonal vectors. In our example above that involves 3D vectors,
-dimensional subspace would involve combining the parts of the vector parallel to each of the orthogonal vectors. In our example above that involves 3D vectors, ![]() and
and ![]() . In higher dimensions, no simple 3D cross products can save you there.
. In higher dimensions, no simple 3D cross products can save you there.
Now we are done with vectors. Let’s take a look at curves!
Curve Approximation
Let’s say our interval of interest is ![]() . Given a 3rd-order polynomial curve
. Given a 3rd-order polynomial curve ![]() , what’s the best approximation using a 2st-order polynomial curve, or a 1th-order polynomial curve (flat line)? How about simply dropping the higher-order terms, so we get
, what’s the best approximation using a 2st-order polynomial curve, or a 1th-order polynomial curve (flat line)? How about simply dropping the higher-order terms, so we get ![]() and
and ![]() ? Here’s what they look like:
? Here’s what they look like:
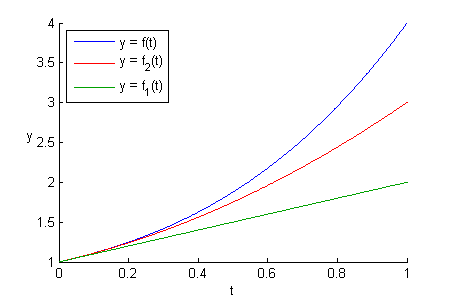
At first glance, I’d say ![]() and
and ![]() are not what we want. We can definitely find a parabolic curve and a line that approximate
are not what we want. We can definitely find a parabolic curve and a line that approximate ![]() better. Look at just how far apart
better. Look at just how far apart ![]() and
and ![]() are from
are from ![]() at
at ![]() . Clearly,
. Clearly, ![]() and
and ![]() are not the 2nd-order and 1st-order polynomial curves that have the least RMSEs from
are not the 2nd-order and 1st-order polynomial curves that have the least RMSEs from ![]() . Simply dropping higher-order terms turns out to be a naive approach. The right way to do it is just like what we did with vectors: projection.
. Simply dropping higher-order terms turns out to be a naive approach. The right way to do it is just like what we did with vectors: projection.
In the vector example above, we were operating in the 3D geometric space. Now we are working with a more abstract 3rd-order polynomial space where ![]() lives in. The lower-order polynomial curve that has the least RMSE from
lives in. The lower-order polynomial curve that has the least RMSE from ![]() is the projection of
is the projection of ![]() into that lower-order polynomial space. Let’s start with finding the 2nd-order polynomial curve that has the least RMSE from
into that lower-order polynomial space. Let’s start with finding the 2nd-order polynomial curve that has the least RMSE from ![]() .
.
The 2nd-order polynomial subspace is 3-dimensional, since a 2nd-order polynomial curve has the form ![]() . Let’s first find 3 curves that span the subspace. An easy pick would be
. Let’s first find 3 curves that span the subspace. An easy pick would be ![]() ,
, ![]() , and
, and ![]() . Now we need to use them to generate a set of orthogonal curves,
. Now we need to use them to generate a set of orthogonal curves, ![]() ,
, ![]() , and
, and ![]() using the Gram-Schmidt process:
using the Gram-Schmidt process:
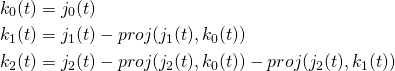
If you forgot how to “project” a curve onto another, please refer to the previous post.
Here are the results:
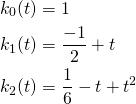
You can say that ![]() ,
, ![]() , and
, and ![]() are a set of orthogonal axes spanning the 2nd-order polynomial subspace. Now we split
are a set of orthogonal axes spanning the 2nd-order polynomial subspace. Now we split ![]() into three orthogonal parts by projecting it onto
into three orthogonal parts by projecting it onto ![]() ,
, ![]() , and
, and ![]() :
:
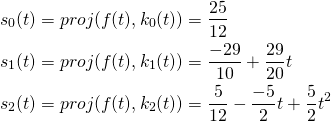
Here’s what ![]() ,
, ![]() , and
, and ![]() look like alongside
look like alongside ![]() :
:
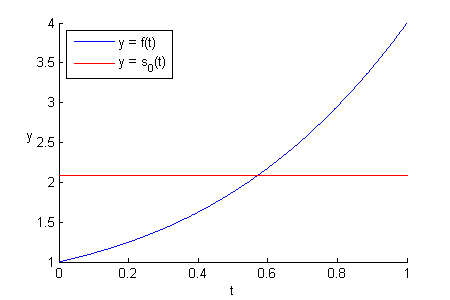
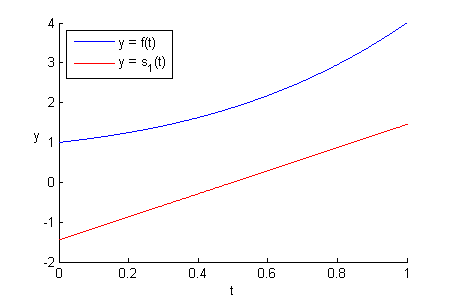
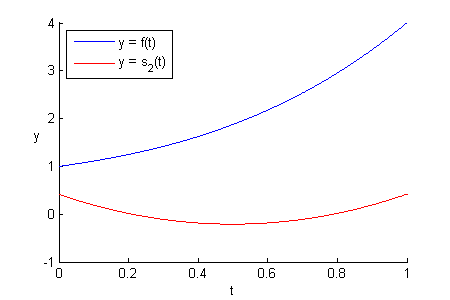
![]() and
and ![]() might not look like they are close to
might not look like they are close to ![]() , but they are the closest curves you can get along the axes
, but they are the closest curves you can get along the axes ![]() and
and ![]() that have the least RMSEs from
that have the least RMSEs from ![]() .
.
Now, we can combine the three orthogonal parts of ![]() to form the 2nd-order polynomial curve that is the best approximation of
to form the 2nd-order polynomial curve that is the best approximation of ![]() :
:
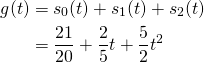
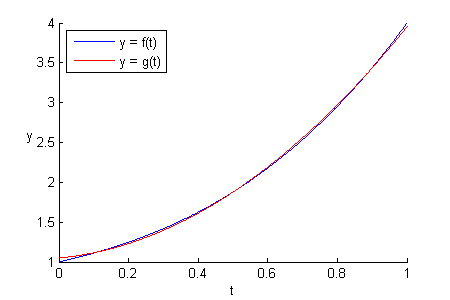
This looks way better than the result of simply dropping the 3rd-order term, as shown in the figure above.
Since the three parts are already orthogonal, we can actually obtain the 1st-order polynomial curve that best approximates ![]() by simply dropping
by simply dropping ![]() from
from ![]() :
:
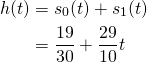
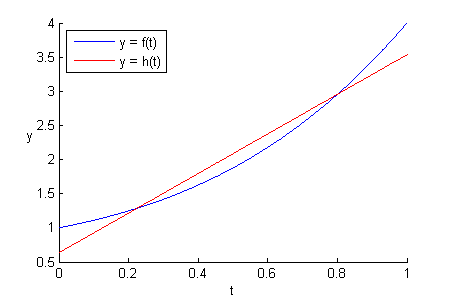
Also looking good, compared to simply dropping the 3rd-order and 2nd-order terms.
That’s it. In this post, we’ve seen how to generate a set of orthogonal curves from a set of curves spanning a lower-dimensional subspace of curves, and use the orthogonal curves to find the best approximation of a curve via curve “projection”.
We now have all the tools we need to move onto Fourier transform and spherical harmonics in the next post. Finally, something game-related!


This is really great! 🙂 When we could expect the next part? I’m not trying to hurry you, I can imagine that writing on such topic is not an easy task (or at least not a quick task). I’m just wondering if you already scheduled the next part? Or is it postpone when you have more time?
It’s on my list. But there are other things going on right now, so it’s currently not my top priority.
I see. Thanks for the quick answer.